jueves, 27 de octubre de 2011

Arboles

Definición
Formalmente, podemos definir un árbol de la siguiente forma:

Caso base: un árbol con sólo un nodo (es a la vez raíz del árbol y hoja).

Un nuevo árbol a partir de un nodo $n r$ y $k$ árboles $A_1, A_2 \dots A_k$ de raíces $n_1, n_2, \dots, n_k$ con $N_1, N_2, \dots ,N_k$ elementos cada uno, puede construirse estableciendo una relación padre-hijo entre $n r$ y cada una de las raíces de los $k$ árboles. El árbol resultante de $N = 1 + N_1 + \dots + N_k$ nodos tiene como raíz el nodo $n r$ , los nodos $n_1, n_2, \dots, n_k$ son los hijos de $n r$ y el conjunto de nodos hoja está formado por la unión de los $k$ conjuntos hojas iniciales. A cada uno de los árboles $A i$ se les denota ahora subárboles de la raíz.

Una sucesión de nodos del árbol, de forma que entre cada dos nodos consecutivos de la sucesión haya una relación de parentesco, decimos que es un recorrido árbol. Existen dos recorridos típicos para listar los nodos de un árbol: primero en profundidad y primero en anchura. En el primer caso, se listan los nodos expandiendo el hijo actual de cada nodo hasta llegar a una hoja, donde se vuelve al nodo anterior probando por el siguiente hijo y así sucesivamente. En el segundo, por su parte, antes de listar los nodos de nivel

n + 1

(a distancia

n + 1

aristas de la raíz), se deben haber listado todos los de nivel

n

. Otros recorridos típicos del árbol son preorden, postorden e inorden:

El recorrido en preorden, también llamado orden previo consiste en recorrer en primer lugar la raíz y luego cada uno de los hijos $A_1, A_2 \dots A_k$ en orden previo.
El recorrido en inorden, también llamado orden simétrico (aunque este nombre sólo cobra significado en los árboles binarios) consiste en recorrer en primer lugar $A 1$ , luego la raíz y luego cada uno de los hijos $A_2 \dots A_k$ en orden simétrico.
El recorrido en postorden, también llamado orden posterior consiste en recorrer en primer lugar cada uno de los hijos $A_1, A_2 \dots A_k$ en orden posterior y por último la raíz.

Tipos de arboles

Árboles Binarios
- Árbol de búsqueda binario auto-balanceable
  - Árboles AVL
  - Árboles Rojo-Negro
  - Árbol AA
Árboles Multicamino

Árboles B (Arboles de búsqueda multicamino autobalanceados)

Árbol-B+
Árbol-B*

Las operaciones comunes en árboles son:

- Enumerar todos los elementos.
- Buscar un elemento.
- Dado un nodo, listar los hijos (si los hay).
- Borrar un elemento.
- Eliminar un subárbol (algunas veces llamada podar).
- Añadir un subárbol (algunas veces llamada injertar).
- Encontrar la raíz de cualquier nodo.
Por su parte, la representación puede realizarse de diferentes formas. Las más utilizadas son:
- Representar cada nodo como una variable en el heap, con punteros a sus hijos y a su padre.
- Representar el árbol con un array donde cada elemento es un nodo y las relaciones padre-hijo vienen dadas por la posición del nodo en el array

Recorridos

Al visitar los nodos de un árbol existen algunas maneras útiles en las que se pueden ordenar sistemáticamente los nodos de un árbol.

Los ordenamientos más importantes son llamados: preorden, post-orden y en-orden y se definen recursivamente como sigue:

Si un árbol T es nulo, entonces, la lista vacía es el listado preorden, post-orden y en-orden del árbol T.

Si T consiste de un sólo nodo n, entonces, n es el listado preorden, post-orden y en-orden del árbol T.

Los algoritmos de recorrido de un árbol binario presentan tres tipos de actividades comunes:

• visitar el nodo raíz

• recorrer el subárbol izquierdo

• recorrer el subárbol derecho

Estas tres acciones llevadas a cabo en distinto orden proporcionan los distintos recorridos del árbol.

Recorrido en PRE-ORDEN:

• Visitar el raíz

• Recorrer el subárbol izquierdo en pre-orden

• Recorrer el subárbol derecho en pre-orden

Recorrido EN-ORDEN

• Recorrer el subárbol izquierdo en en-orden • Visitar el raíz • Recorrer el subárbol derecho en en-orden

Recorrido en POST-ORDEN

• Recorrer el subárbol izquierdo en post-orden

• Recorrer el subárbol derecho en post-orden

• Visitar el raíz

Clases de arbol

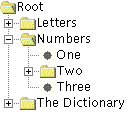
Con la clase JTree, se puede mostrar un árbol de datos. JTree realmente no contiene datos, simplemente es un vista de ellos. Aquí tienes una imagen de un árbol.

Como muestra la figura anterior, JTree muestra los datos verticalmente. Cada fila contiene exactamente un ítem de datos (llamado un nodo). Cada árbol tiene un nodo raíz (llamado Root en la figura anterior, del que descienden todos los nodos. Los nodos que no pueden tener hijos se llaman nodos leaf (hoja). En la figura anterior, el aspecto-y-comportamiento marca los nodos hojas con un círculo.
Los nodos que no sean hojas pueden tener cualquier número de hijos, o incluso no tenerlos. En la figura anterior, el aspecto-y-comportamiento marca los nodos que no son hojas con un carpeta. Normalmente el usuario puede expandir y contraer los nodos que no son hojas -- haciendo que sus hijos sena visibles o invisibles -- pulsando sobre él. Por defecto, los nodos que no son honas empiezan contraidos.
Cuando se inicializa un árbo, se crea un ejemplar de TreeNode para cada nodo del árbol, incluyendo el raíz. Cada nodo que no tenga hijos es una hoja. Para hacer que un nodo sin hijos no sea una hoja, se llama al método setAllowsChildren(true) sobre él.

jueves, 13 de octubre de 2011

Programa con y sin menu

SIN MENU

CON MENU

Colas..

COLAS

Definición:

Son aquellas que solo tiene 2 operaciones, Push(Inserción) y Pop(Eliminación). Push solo se puede efectuar por un extremo llamado Frente y Pop por el extremo Llamado Final. Sin Embargo se le pueden aplicar todas las operación al igual que a las listas.

Tipos de colas:

Colas circulares (anillos): en las que el último elemento y el primero están unidos.

Colas de prioridad: En ellas, los elementos se atienden en el orden indicado por una prioridad asociada a cada uno. Si varios elementos tienen la misma prioridad, se atenderán de modo convencional según la posición que ocupen. Hay 2 formas de implementación:

Añadir un campo a cada nodo con su prioridad. Resulta conveniente mantener la cola ordenada por orden de prioridad.
Crear tantas colas como prioridades haya, y almacenar cada elemento en su cola.

Bicolas: son colas en donde los nodos se pueden añadir y quitar por ambos extremos; se les llama DEQUE (Double Ended QUEue). Para representar las bicolas lo podemos hacer con un array circular con Inicio y Fin que apunten a cada uno de los extremos. Hay variantes:

Bicolas de entrada restringida: Son aquellas donde la inserción sólo se hace por el final, aunque podemos eliminar al inicio ó al final.

Bicolas de salida restringida: Son aquellas donde sólo se elimina por el final, aunque se puede insertar al inicio y al final.

Recorrido

Definición:

Ya que las colas son FIFO(First in - First Out) el Recorrido se hace sacando el primer dato que se inserto hasta que llegue al extremo llamado Final.

Push

Definición:

Push es simplemente el método por el cual va agregando un Dato nuevo a la Cola tomando en cuenta el Tamaño Máximo de Capacidad (Max), el Frente y el Final de la Cola.

Detalle:

Primer nos aseguramos que la Cola no este Llena, para que de esta manera sea capaz de insertar un Elemento nuevo. Si no desplegara Cola Llena. Después compara para determinar las posicionesde Frente y Final y de esta manera poder moverlo con libertad. Ya que determina los valores de Frente y Final, nos Indica que Cola[Final] tomara el valor de Elemento.

Pop

Definición:

Pop es simplemente el método por el cual va sacando el primer Dato de la Cola (esto se comprueba ya que las Colas son FIFO), para esto toma en cuenta el Frente.

Detalle:

Compara para determinar si la cola esta vacía, de otra forma lo que hace es Imprimir “Eliminando el Dato…”. Después se hacen una series de comparaciones para determinar la nueva posición deFrente, de esa forma el Dato que existía en Frente es Eliminado.

Programa de colas

martes, 4 de octubre de 2011

PIlas Java!!

Pilas

Una pila (stack en inglés) es una lista ordinal o estructura de datos en la que el modo de acceso a sus elementos es de tipo LIFO (del inglés Last In First Out, último en entrar, primero en salir) que permite almacenar y recuperar datos. Esta estructura se aplica en multitud de ocasiones en el área de informática debido a su simplicidad y ordenación implícita de la propia estructura.

Para el manejo de los datos se cuenta con dos operaciones básicas: apilar (push), que coloca un objeto en la pila, y su operación inversa, retirar (o desapilar, pop), que retira el último elemento apilado.

En cada momento sólo se tiene acceso a la parte superior de la pila, es decir, al último objeto apilado (denominado TOS, Top of Stack en inglés). La operación retirar permite la obtención de este elemento, que es retirado de la pila permitiendo el acceso al siguiente (apilado con anterioridad), que pasa a ser el nuevo TOS.

Por analogía con objetos cotidianos, una operación apilar equivaldría a colocar un plato sobre una pila de platos, y una operación retirar a retirarlo.
Las pilas suelen emplearse en los siguientes contextos:

Evaluación de expresiones en notación postfija (notación polaca inversa).
Reconocedores sintácticos de lenguajes independientes del contexto
Implementación de recursividad

Operaciones

Una pila cuenta con 2 operaciones imprescindibles: apilar y desapilar, a las que en las implementaciones modernas de las pilas se suelen añadir más de uso habitual.

Crear: se crea la pila vacía.
Apilar: se añade un elemento a la pila.(push)
Desapilar: se elimina el elemento frontal de la pila.(pop)
Cima: devuelve el elemento que esta en la cima de la pila. (top o peek)
Vacía: devuelve cierto si la pila está vacía o falso en caso contrario.

EJEMPLO